【摘 要】 推进教学公平,让儿童平等地获得最大程度地发展是每个学习者不可剥夺的基本学习权利。在公平视域中反思当前的课堂教学,学生话语权的缺失无疑是一个值得关注和应该引起重视的问题。本文通过来自课堂的观察研究,深入真实的课堂教学实践,从数学课堂学生话语权的缺失现状、意义寻绎、特征阐述、实践建构等方面进行了分析描述,旨在重构一种基于公正性、主体性和发展性的学生话语权,促进学生话语权的理性回归。
【关键词】 课堂教学公平 学生话语权 缺失 寻绎 重构
随着教育公平问题研究的深入,对其争鸣的焦点正在发生着悄然的转移:由宏观走向微观,由地域走向课堂,由决策者到教育者预示着教育公平探讨的新走向。课堂教学是师生双方进行对话和交往的过程,课堂教学公平问题无时无刻不体现在师生的课堂话语上。对课堂来说,教师和学生理论上是平等的,享有共同的话语权,而实际上课堂的话语权属于教师与部分优秀的学生。学生公平话语权的缺失无疑是一个值得关注和应该引起重视的问题,在课程文化转型下,教师应着力于教师话语霸权的消解以及教师和学生话语权的共享,将公平的精神植根于课堂,尊重儿童的表达和交流权利,倾听每个儿童的声音,让每个儿童真切地感受到教师对他们的平等关怀,是课堂教学的本真要义。
一、行进——学生话语权缺失的真实考量
从个体的主体地位讲,教师与儿童都是独立的个体,都有自己独立言说的话语权利。可是由于教育的某种“异化力量”,学生的话语权屡遭缺失。
(一)教师话语霸权:主宰儿童的声音
为剖析现行小学数学课堂学生话语权的缺失现状,我们以本校10位数学老师执教的10节数学课为研究对象,通过随堂观察、记录和录音,对10位教师的课堂话语进行统计和定量、定性分析。
表1 数学课堂话题情况统计表
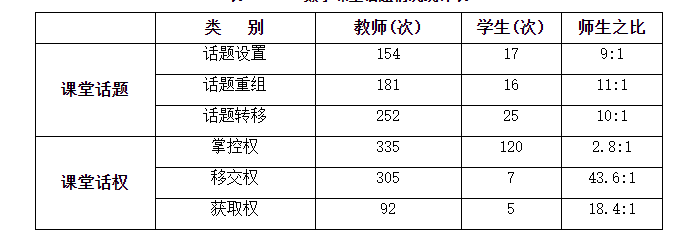
从上表可知,无论是话题设置、重组、转换,还是话权的掌控、移交、获取,教师都处于强势地位,学生处于弱势,明显表现为权力的不对称。正因为有这些优势,教师在课堂教学中常常处于核心地位,进而可能演变为话语霸权。这一点我们可以从问答过程中的话题设置、重组(包括推进)、转换、话权掌控、移交、获取的视角得到清晰的探查。也就是说,在数学课堂中,教师通过掌握话题设置、重组、转换的权力,通过话权掌控、移交、获取来掌握教学的主动权,这些权力使用得过度和僭越,就形成了话语霸权。
(二)学生话语地位失衡:主宰弱势群体的声音
在课堂上,那些反应敏捷、表达清晰的优秀生总会频繁抢得有限的学生话语权,成为课堂教学顺畅进行的助推器。反之,其他学生则在有限的话语分配中再次丧失主动权。我们通过课堂观察,选择学生回答话语的次数这一视角进行统计、分析和研究,制订出统计表,旨在研究随意发挥的学生话语次数在一节课上的分布状况,了解每个学生的话语权,改进学生之间话语权不平的现状。现选一节校普通教师的课来加以说明。
表2:学生课堂话语次数统计表
研究内容:本校老师《分数的基本性质》
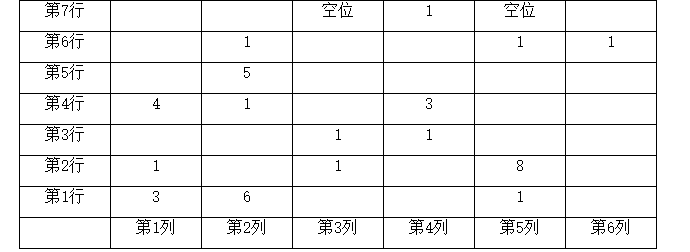
说明:
1.教室内实有学生40人,表格中的数字为该位置的学生话语的次数;2.学生话语率为95%。(学生话语率=参与话语的总次数÷学生总数×100%)3.话语覆盖面为40%。(话语覆盖率=参与话语的学生人数÷学生总数×100%)
上表中学生话语率为95%,话语覆盖面为40%;学生话语率与话语覆盖率之间的差值,体现了重复话语的情况,上表中差值较大,说明重复话语的次数较多,像上表中的学生(5,2)就被重复叫了8次。除学生话语的覆盖面不广这一问题外,另一个重要的问题是课堂上经常会有被教师遗忘的角落。如本课中学生(3,5)、(3,6)、(4,5)、(4,6)所在的四个位置形成的矩形区域,就是一个被遗忘的角落。长此以往,势必影响处于劣势的学生的话语积极性,进而阻碍其进一步的话语权实现。
二、解读——学生话语权的意义寻绎
在后现代的哲学视野里,儿童的声音是非常重要的。声音代表一个人的权利,尤其是话语的权利。后现代哲学家福柯在《关于语言的话语》中,曾精辟地论述了话语与权利之间的关系。他说:“话语是一种权利关系,它意味着谁有发言权,谁无发言权”。他认为:话语中隐含着权利,话语的实践隐含着权利的运用,而权利实际上是基于特定的社会背景和情境的一种控制关系和行为。
话语权是学生神圣的天赋之权。学生的话语权是指学生在数学学习中有权自由表达自己的观点和意愿,有权与教师合作对话,有权对数学教材与数学学习的内容进行质疑、加工和再创造。学生的话语权是通过学生在数学课堂教学中的地位获得而确立的、它是学生作为“人”所本应具有的权利。
三、深入——公平视域下学生话语权的特征阐述
(一)公正性
公正是公平视域下学生话语权的首要特征,因为“公正最为完全,它是交往行为上的总体的德性。”话语公正意味着教师应将学生置于一个平等的社会位置中,依据和尊重学生个体差异的相对平等,为每一个学生提供他所需要的话语的权利。
(二)主体性
主体性主要表现在自由、自主和创造性三个方面。其中自由是基础,自主是表现,创造性是主体性的最高追求。所谓自由的话语是指学生在数学课堂中能尽情地表达自己的思想而不受约束;自主的话语是指学生发自内心深处的真实情感的表达,而不是替别人或权威说话;创造性的话语是基于前面二者之上的更高的层次,它要求学生发挥意识的能动作用,想别人之未想,说别人之未说,是学生主体能动性的集中表现。
(三)发展性
假如说公正性是学生话语权的表现形式,自由性是其保障的话,那么发展性就是学生话语权的目标。这种发展性要求学生的话语在一定积累基础上有着主动性和创造性,而不是被动地因循守旧,不敢突破创新。只有这样才能使学生自身获得最大最快发展,使课堂话语体系更加科学完善,使社会获得不断进步。
四、实践——学生话语权重构的有效践行
为了学生的发展,我们呼唤师生话语权的共享与平等,呼唤学生话语权的重构,把课堂净化为一个充满勃勃生机的富有生命力的发展课堂。
(一)消除权威——解构教师的话语霸权
话语权要想由教师独自享有转为由全体儿童共同拥有,就必须消解教师的话语中心,使课堂权力格局由带有等级秩序、封闭性、单向度的形态转向平等的、活跃的、多向开放的形态。教师不能再以自我权威为中心,要承认儿童主体的话语权利,给予儿童质疑教师的权利,参与讨论的权利,发表自己观点的权利,提出建议的权利等,使儿童从过去依附教师话语的地位走向自我言说的自由,使课程教学活动因“儿童”的言说而存在,而富有意义。
【案例1】 听他把话讲完,或许能豁然开朗
“长方体表面积”的教学片断:
出示题目:一个长方体的长、宽、高分别是10厘米、5厘米、5厘米,求它的表面积。
师:请同学们根据这个长方体的数据列式计算这个长方体的表面积。
生1:(5×10+5×5+10×5)×2
生2: 5×10×2+5×5×2+10×5×2
生3: 5×10×4+5×5×2
……
生4:老师,我还有一种算法,算法是5×10×5。
生5:“题目要求的是长方体的表面积,不是求体积,”其他同学都笑了。
生4:老师,我是求长方体表面积的。
师:你能把你的想法说给大家听一听吗?
生4拿起一个长方体学具,指着说:“长方体的一个侧面积是5×10,我把它当作2个5×5,那么4个侧面就是8个5×5再加上上下两个底面积2个5×5,这样这个长方体的表面积一共就有10个5×5,即:5×5×10。
(短暂地沉默后,教室立即响起了掌声。)
又一位同学站起来说:“老师我也有一种新的解法,列式是5×10×5。”
师:方法是对的,这位同学根据乘法交换律,交换了因数的位置,其实方法是一样的。
生6:老师,不对,我的解法和刚才不一样。
师:那你说说你的方法。
生6:我是把底面积转化成侧面积来计算的,两个底面积的和刚好等于一个侧面积,长方体表面积一共有5个5×10,所以列式是5×10×5。
(掌声又一次响起。)
师:你们真是聪明的孩子,这两种方法连老师都没想到,谢谢你们!
“长方体表面积”教学顺顺当当进行中,前面几位学生的方法都很浅显易懂,生4的方法“5×5×10”将师生引向异处:这不是长方体的体积计算公式吗?此时的教师完全可以利用自己的“权威”立即加以否定,使课堂“一帆风顺”。值得庆幸的是,教师“耐心沉着的期待”,不但允许生4、生6把话讲完,还能勇敢地承认自己的错误。没有了“教师权威”的干涉,学生拥有了更多的话语权,学生的思维在民主的氛围中得以碰撞与提升,课堂也完全因学生的智慧生长而灵动生成。
(二)重建机制——激励学生的自我话语权
学生话语权的重构,需要学生自我意识的觉醒,需要实现话语机制的重建,构建一套师生之间的言说方式和规约,如,话题设置、重组、转换和话权掌控、移交、获得的基本权利与义务、方法与要求等。除此之外,还要在数学课堂上关注学生基本能力的培养,如:提问与应答的能力,沟通与交流的能力,话题的拾取,话权的获得,话语机会的把握等,这些都是需要学习与掌握的能力。
【案例2】 给孩子一个权利,还课堂生动与灵气
“加法结合律”的教学片段:
……
生1:“我觉得加法交换律等号左边(a+b)+c只要写成a+b+c就可以了,这儿的括号可以不加。”
师:“生1认为这儿的括号可以不加,同意他的观点吗?”
一席话引起了全班的议论:“对呀,反正先算a+b,括号不用也可以。
生2:“那现在该怎样表示加法结合律呢?”
生3:“a+b+c=a+(b+c)”
生4:“我觉得加法中谁和谁先加都可以,所以a+b+c=a+(b+c)=b+(a+c)
生5:“又有交换又有结合,看来不能叫结合律了,那该叫什么呢?”
生6:“这条定律中还运用了加法交换律,我们可以叫它加法任意运算定律!”
生7:“任意运算定律,怎么用文字表述呢?”
生8:“三个数相加,把其中任意两个数相加,再加第三个数,和不变。”
生9:“我觉得不止三个数,更多也可以,几个数相加,先把几个数相加,再和一个数相加,和不变。”
生10:“不好不好,不够准确”。
生11:“可以这样说:几个数相加,先把其中一些数相加,再和剩下的数相加,和不变。”
师:“真了不起!这就是加法的任意运算定律,是你们自己发现的,就叫四(1)定律吧。”
在这里,生1根据自己在学习中的发现,设置“这儿的括号可以不加”这一话题,教师及时抓住了学生的话题,以 “生1认为这儿的括号可以不加,同意他的观点吗?”把话题的掌控权移交给学生,生2和生5和生7又及时地转换话题,整个环节的话题权都在学生手里,学生有了言说的权利、思维的空间、交流的机会,课堂也因此变得充满活力。
(三)和而不同——提升学生的质疑话语权
数学课堂中教师要给学生“真正的话语权”,就要正视学生的“不同”,鼓励学生与自己观点相一致的同学交流,寻找对自己观点的有力支持,也可以寻找与自己观点不一致的同学理论,说服别人或修正自己。在这样的争论中,学生才有自己的“话语权”,才能在观点的碰撞中闪烁出智慧的火花。
【案例3】 大家都乐于争论,课堂才会精彩
“轴对称图形”的教学片断:
师:想不想知道以前学过的图形,哪些是轴对称图形?生(齐):想!
师:请同学们打开信封,拿出表格与图形,通过折折图形完成表格内的填空。(注:表格里涉及图形名称、是不是轴对称图形、有几条对称轴三项内容)
学生以小组为单位活动,老师巡视并参与到小组学习中。
结果,各小组在汇报的过程中,对于三角形是不是轴对称图形分成了两种意见:一种认为三角形是轴对称图形,另一种认为不是。
师(笑着):谁是谁非,大家来个辩论赛吧!认为是的为正方,认为不是的为反方。现在,两方选代表上台陈述理由吧。
生(正方):大家请看,我们组的三角形经过对折,折痕两边能完全重合,证明三角形确实是轴对称图形。正方学生立刻发出援助声:“耶——”
生(反方):同学们看好了,我们组的三角形折来折去,折痕两边就是不重合,说明三角形不是轴对称图形。不信,你来试试!(反方发出了挑战)这时,反方学生也发出了支持信号:“不是——不是——不是,耶——”
正方学生代表不服气地接过反方的三角形,试了半天,折痕两边就是不重合。
这时,教室可安静了,因为同学们的眼睛都在望着老师。
生(台下):两个三角形不一样!(他的声音像一声响雷打破了沉静)
师(惊讶):怎么不一样了?
生(台下):正方是一个是等腰三角形,而反方的不是等腰三角形。
此时,学生们才发现,老师放在信封中的三角形是不一样的:原来等腰三角形是轴对称图形,而非等腰三角形不是轴对称图形。
师(微笑):完全正确!还有什么想法?
生:我认为等边三角形也是轴对称图形,它应有3条对称轴。
师(高兴):那我们快来验证一下吧!
上述案例中,老师在信封中放入不同的三角形,别具匠心地设置了自相矛盾的“陷阱”,巧妙地创设了一个学生争论的机会,每个孩子都可以陈述自己的观点,学生在“辩论”中知识得到重组,观念得到沟通,思想得到碰撞情感得到交融。有争论,才能相互促进,这是课堂教学的“相生”之道,这种争论是建立美好的“和而不同”教学的基石。
(四)不弃主义——扩大学生的自主话语权
“常善救人,故无弃人;常善救物,故无弃物”,老子这种“不弃主义”的教育思想,就是当代社会所倡导的教学公平。教学公平是现代教育的本性的存在方式,也是现代教育的基本原则。教学公平意味着每个学生应享有平等的话语言说的权利。实践中,我们经常会看到,课程教学活动中发言积极、话语比较多的儿童总是那些发展程度相对较高、性格比较外向的儿童。教学活动中他们的言语几乎占据了儿童话语的全部,而那些“弱势群体”儿童则几乎没有声音。所以构建民主、多元话语的课程教学活动,教师就有必要去关注他们的声音,在放下自己话语权威的同时,去倾听这些儿童的心声,了解他们的心理,捕捉他们内心深处的欲望与需求,体会他们的感受,采取积极措施调动他们参与教学活动的积极性,唤醒他们的话语意识,使他们轻松地发出自己的独特声音,拥有更多的言说机会,使教学活动成为全体儿童“共声喧哗”的活动。
结 语
当学生不是为教师而言说,而是为自己而言说的时候;当课堂上听到的不是一种声音,而是涌动着多种声音,交汇着多种智慧的时候,真正的自由民主发展和充满生命气息与创造力的课堂才会真正呈现,只有这样,学生的话语权才能实现真正意义上的回归与重构。
参考文献
[1] [美]帕特里夏·奥坦伯德·约翰逊.阿伦特.世界思想家译丛[M].王永生译.北京:中华书局,2006.99,117,117.
[2] 王春燕.声音·话语·权利[J].幼儿教育,2004,(12).
[3] 郑乐平.超越现代主义和后现代主义——论新的社会理论空间之建构.上海:上海教育出版社,2003.
[4] 彭文秀.“引”与“放”新课改中课堂教学话语权分析.当代教育科学,2005,13(29).
[5] 龚振.讨论:把话语权还给学生[J].广西:基础教育研究,2002(2).